2020暑期学生练习-第四周-2020暑期每周练习-04
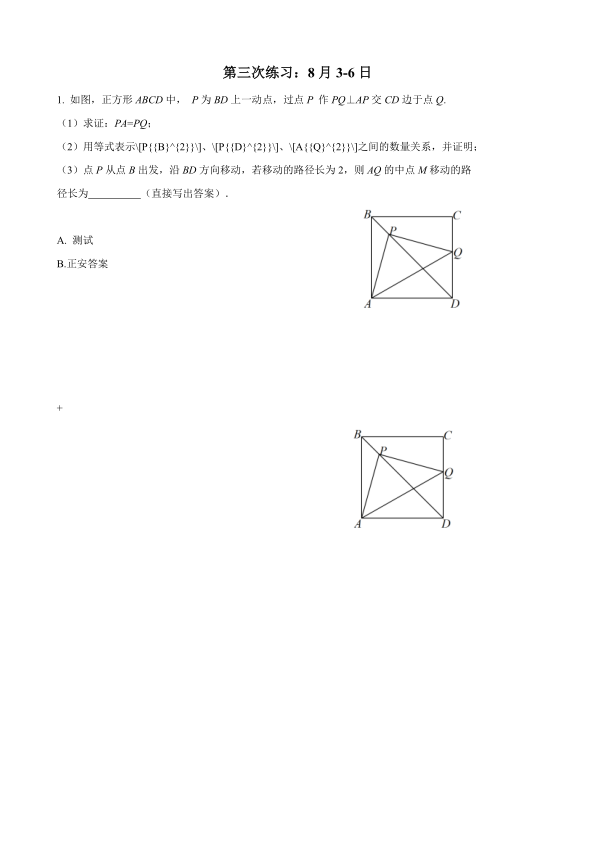
第三次练习:8月3-6日 1. 如图,正方形\(ABCD\)中, \(P\)为\(BD\)上一动点,过点\(P\) 作\(PQ\)⊥\(AP\)交\(CD\)边于点Q. (1)求证:\(PA\)=\(PQ\); (2)用等式表示\(P{{B}^{2}}\)、\(P{{D}^{2}}\)、\(A{{Q}^{2}}\)之间的数量关系,并证明; (3)点\(P\)从点\(B\)出发,沿\(BD\)方向移动,若移动的路径长为2,则\(AQ\)的中点\(M\)移动的路 径长为 (直接写出答案). A. 测试 B.正安答案 + (1)证明:过点\(P\)作\(PE\bot AD\)于点\(E\),\(PF\bot CD\)于点\(F\). ∴\(\angle PED=\angle PEA=\angle PFD={{90}^{\circ }}\). ∵四边形\(ABCD\)是正方形, ∴\(\angle ADC=90{}^\circ ,\angle ADB=\angle CDB={{45}^{\circ }}\). ∴\(PE=PF\). ∴\(PEDF\). .………………………………1分
\(\frac{a}{b}\pm \frac{c}{d}= \frac{ad \pm bc}{bd} \hdotsfor{n} \)
\hdotsfor{n}
第3章 函数
第1课时 平面直角坐标系
【学习目标】
(1)认识并能画出平面直角坐标系;在给定的直角坐标系中,会根据坐标描出点的位置,由点的位置写出它的坐标.
(2)能在方格纸上建立适当的直角坐标系,描述物体的位置;能结合具体情境灵活运用多种方式确定物体的位置.
(3)在同一直角坐标系中,感受图形变化后点的坐标的变化和各点坐标变化后图形的变化.
【学习过程】
一、考点精讲
{'width': 151, 'height': 145, 'name': 'image126.png'} 1.点的坐标
对于平面内任意一点\( P \),过点\( P \)向\( x \)轴、\( y \)轴作垂线,垂足在\( x \)轴、\( y \)轴上对应的数\( a \),\( b \)分别叫做点\( P \)的{'width': 151, 'height': 145, 'name': '\n'} 和{'width': 151, 'height': 145, 'name': ''} ,有序数对\( (a,b) \)叫做点\( P \)的坐标,记作{'width': 151, 'height': 145, 'name': '\n'} .坐标轴上的点不属于{'width': 151, 'height': 145, 'name': ''} .{'width': 151, 'height': 145, 'name': ''}
2.点到坐标轴的距离
点\( P(a,b) \)到\( x \)轴的距离是点的纵坐标的绝对值,即{'width': 151, 'height': 145, 'name': ''} ;
点\( P(a,b) \)到\( y \)轴的距离是点的横坐标的绝对值,即{'width': 151, 'height': 145, 'name': ''} .
3.各象限中及坐标轴上点的坐标各象限中点的坐标
点\( P(x,y) \)在第一象限\( ⇔ \){'width': 151, 'height': 145, 'name': ''} ;点\( P (x,y) \)在第二象限\( ⇔ \){'width': 151, 'height': 145, 'name': ''} ;
点\( P(x,y) \)在第三象限\( ⇔ \){'width': 151, 'height': 145, 'name': ''} ;点\( P (x,y) \)在第四象限\( ⇔ \){'width': 151, 'height': 145, 'name': ''} .
坐标轴上点的坐标
点\( P(x,y) \)在\( x \)轴上\( ⇔ y=0 \),\( x \)为任意实数;
点\( P(x,y) \)在\( y \)轴上\( ⇔ x=0 \),\( y \)为任意实数;
点\( P(x,y) \)既在\( x \)轴上,又在\( y \)轴上\( ⇔ x=0 \),\( y=0 \),即点\( P(x,y ) \)的坐标为\( (0,0) \).
平行于坐标轴的直线上的点
平行于\( x \)轴直线上的两点,其纵坐标{'width': 151, 'height': 145, 'name': ''} ,横坐标{'width': 151, 'height': 145, 'name': ''} ;
平行于\( y \)轴直线上的两点,其横坐标{'width': 151, 'height': 145, 'name': '\n'} ,纵坐标{'width': 151, 'height': 145, 'name': ''} .
4.点的变换
(1)两点关于\( x \)轴对称\( ⇔ \)两点坐标横坐标{'width': 151, 'height': 145, 'name': ''} ,纵坐标{'width': 151, 'height': 145, 'name': '\n'} ;
(2)两点关于\( y \)轴对称\( ⇔ \)两点坐标横坐标{'width': 151, 'height': 145, 'name': ''} ,纵坐标{'width': 151, 'height': 145, 'name': '\n'} ;
(3)两点关于原点对称\( ⇔ \)两点坐标横坐标{'width': 151, 'height': 145, 'name': ''} ,纵坐标{'width': 151, 'height': 145, 'name': '\n'} .
(4)左右平移:向右平移,横坐标增大,纵坐标不变;向左平移,横坐标减小,纵坐标不变;
(5)上下平移:向上平移,纵坐标增大,横坐标不变;向下平移,纵坐标减小,横坐标不变。
5.平面直角坐标系内两点间的距离
若点A(x\( _1 \),y\( _1 \)),B(x\( _2 \),y\( _2 \)),则AB之间的距离可以表示为 ______________.
{'width': 156, 'height': 162, 'name': 'image127.png'} 二、中考真题
1. (2015北京8题3分)如图是利用平面直角坐标系画出的故宫博物院的主要建筑分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示太和门的点的坐标为(0,-1),表示九龙壁的点的坐标为(4,1),则表示下列宫殿的点的坐标正确的是( ) A. 景仁宫(4,2) B. 养心殿(-2,3) C. 保和殿(1,0) D. 武英殿(-3.5,-4)
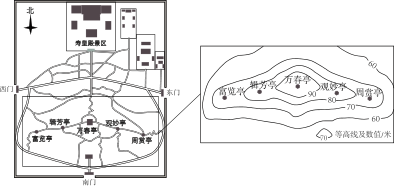
{'width': 204, 'height': 187, 'name': 'image128.png'} {'width': 204, 'height': 187, 'name': 'image129.png'} 2. (2018北京8题2分)上图是老北京城一些地点的分布示意图.在图中,分别以正东、正北方向为x轴、y轴的正方向建立平面直角坐标系,有如下四个结论:
①当表示天安门的点的坐标为(0,0),表示广安门的点的坐标为 (-6,-3)时,表示左安门的点的坐标为(5,-6);
②当表示天安门的点的坐标为(0,0),表示广安门的点的坐标为 (-12,-6)时,表示左安门的点的坐标为(10,-12);
③当表示天安门的点的坐标为(1,1),表示广安门的点的坐标为 (-11,-5)时,表示左安门的点的坐标为(11,-11);
④当表示天安门的点的坐标为(1.5,1.5),表示广安门的点的坐 标为(-16.5,-7.5)时,表示左安门的点的坐标为(16.5,-16.5).
上述结论中,所有正确结论的序号是( ) (A)①②③ (B)②③④ {'width': 184, 'height': 124, 'name': 'image130.png'} {'width': 184, 'height': 124, 'name': 'image131.png'} (C)①④ (D)①②③④
3. (2016北京9题3分)如图,直线mn,在某平面直角坐标系中,x轴\( ∥ \) m,y轴\( ∥ \)n,点A的坐标为(-4,2),点B的坐标为(2,-4),则坐标原点为( )
(A) O\( _1 \) (B) O\( _2 \) (C) O\( _3 \) (D) O\( _4 \)
4. (2014北京12题4分) 在平面直角坐标系xOy中,对于点
P(x,y), 我们把点P\( ' \)(-y+1,x+1)叫做点P的伴随点已知点A\( _1 \)的伴随点为A\( _2 \),点A\( _2 \)的伴随点为A\( _3 \),点A\( _3 \)的伴随点为A\( _4 \),?,这样依次得到点A\( _1 \), A\( _2 \), A\( _3 \),?, A\( _n \),? 若点A\( _1 \)的坐标为
(3,1),则点A\( _3 \)的坐标为______, 点A\( _2014 \)的坐标为 ______; 若点A\( _1 \)的坐标为(a,b), 对于任意的正整数n, 点A\( _n \)均在x轴上方, 则a, b应满足的条件为______.
三、练习提升
{'width': 115, 'height': 101, 'name': 'image132.png'} 考点一:建立平面直角坐标系,确定点的位置
1.数学课上,王老师让同学们对给定的正方形ABCD,建立合适的平面直角坐标系,并表示出各顶点的坐标.下面是4名同学表示各顶点坐标的结果:
甲同学:A(0,1),B(0,0),C(1,0),D(1,1);
乙同学:A(0,0),B(0,-1),C(1,-1),D(1,0);
丙同学:A(1,0),B(1,-2),C(3,-2),D(3,0);
丁同学:A(-1,2),B(-1,0),C(0,0),D(0,2);
上述四名同学表示的结果中,四个点的坐标都表示正确的同学是( )
A.甲、乙、丙 B.乙、丙、丁 C.甲、丙 D.甲、乙、丙、丁
{'width': 232, 'height': 120, 'name': 'image133.png'} 2.右图是玉渊潭公园部分景点的分布示意图,在图中,分别以正东、正北方向为x轴、y轴的正方向建立平面直角坐标系,当表示西桥的点的坐标为\( (- 1pt 1pt 1pt 61) \),表示中堤桥的点的坐标为\( (12) \)时,表示留春园的点的坐标为 ___________.
{'width': 245, 'height': 120, 'name': 'image134.png'} 3.为了保障艺术节表演的效果,某校在操场中标记了几个关键位置,如图所示,利用平面直角坐标系画出的关键位置分布图,若这个坐标系分别以正东、正北方向为\( x \)轴、\( y \)轴的正方向,表示点A的坐标为\( (1, . . -1) \),表示点B的坐标为\( (32) \),则表示其他位置的点的坐标正确的是( )
(A) C\( (-1 . . 0) \) (B) D\( (- 3. . 1) \)
(C) E\( (- 2. -. 5) \) (D) F\( (5. . 2) \)
{'width': 146, 'height': 147, 'name': 'image135.png'}
考点二:根据距离和方向确定点的位置
1.如图,点A在观测点的北偏东方向30 \( ^∘ \),且与观测点的距离为8千米,将点A的位置记作
A(8,30\( ^∘ \)),用同样的方法将点B,点C的位置分别记作
B(8,60\( ^∘ \)),C(4,60\( ^∘ \)),则观测点的位置应在( )
(A) O\( _1 \) (B) O\( _2 \) (C) O\( _3 \) (D) O\( _4 \)
{'width': 176, 'height': 121, 'name': 'image136.png'} 2.如图,这是怀柔地图的一部分,分别以正东、正北 方向为x轴、y轴正方向建立直角坐标系.规定: 一个单位长度表示1km,北京生存岛实践基地A处的坐标是(2,0),A处到雁栖湖国际会展中心B处相距4km,且A在B南偏西45\( ^∘ \)方向上,则雁栖湖国际会展中心B处的坐标是____________.
{'width': 102, 'height': 91, 'name': 'image138.png'}
3.如图,在平面直角坐标系中,点\( A (30) \),判断在\( MNPQ \)四点中,
满足到点\( O \)和点\( A \)的距离都小于2的点是__________.
{'width': 216, 'height': 179, 'name': 'image139.png'} 考点三:平面直角坐标系中点的变换
1.如图,\( △ \)DEF是\( △ \)ABC经过某种变换后得到的图形.
\( △ \)ABC内任意一点M的坐标为(x, y),点 M
经过这种变换后得到点 N,点N的坐标是( ) A.\( -y,-x \) B.\( -x,-y \) C.\( -x,y \) D.\( x,-y \)
{'width': 152, 'height': 121, 'name': 'image140.png'} 2.如图,将线段AB绕点O顺时针旋转90\( ^∘ \)得到线段A\( ' \)B\( ' \),那么A(﹣2,5)的对应点A\( ' \)的坐标是( ). A.(2,5) B.(5,2) C.(2,﹣5) D.(5,﹣2)
3. 在平面直角坐标系xOy中,\( △ \)ABC的顶点分别为A(1,1),B(2,4),C(4,2).
(1) 画出\( △ \)ABC关于原点O对称的\( △ \)A\( _1 \)B\( _1 \)C\( _1 \);
{'width': 172, 'height': 176, 'name': 'image141.png'} (2) 点 C关于x轴的对称点C\( _2 \)的坐标为__________;
(3) 点C\( _2 \)向左平移m个单位后,落在\( △ \)A\( _1 \)B\( _1 \)C\( _1 \)
内部,写出一个满足条件的m的值: __________.
四、课堂总结
本节课你有什么收获,在解决问题中需要注意什么?
第2课时 函数与图象
【学习目标】
(1)了解函数的概念和三种表示方法,能举出函数的实例.
(2)能结合图象对简单实际问题中的函数关系进行分析.
【学习过程】
一、考点精讲
(1)了解生活中一个变量随另一个变量变化而变化的情况.
(2)函数的定义:设在某变化过程中有变量x和y,如果对于变量x在某一范围内的每一个确定的值,y都有 值和它对应,那变量y就叫做变量x的函数. (3)函数的表示方法:解析法、列表法、图象法. (4)自变量的取值范围的确定方法 求某一函数自变量的取值范围,首先,要考虑自变量的取值必须使解析式有意义. ①当自变量以整式形式出现,自变量取值范围是 ; ②当自变量以分式形式出现,自变量取值范围是使分母 的实数; ③当自变量以偶次方根形式出现,自变量取值范围是使被开方数为 数,当自变量以奇次方根出现时,自变量取值范围为 ; ④当自变量出现在零次幂或负整数次幂的底数中,自变量的取值范围是使底数不为零的数.
其次,当函数解析式表示具有实际意义或几何意义的函数时,自变量取值范围除应使函数解析式有意义外,还必须符合实际意义或几何意义. (注意:自变量的取值范围有无限的,也有有限的,还有是单独一个(或几个)数的;在一个函数关系式中,同时有几种代数式,函数的自变量取值范围应是各种代数式中自变量取值范围的 部分.) (5)函数的图象 画函数的图象,一般按下列步骤进行:列表、描点、连线.画函数图象时要注意自变量的取值范围,当图象有端点时,要注意端点是否有等号,有等号时画 点,无等号时画 点.
二、中考真题
1. 小云在学习过程中遇到一个函数\( y=1/6 |x|x^2 -x+1(x≥ -2)^ . \) 下面是小云对其探究的过程,请补充完整: (1)当-2\( ≤ \)x<0时, 对于函数y\( _1 \)={'width': 172, 'height': 176, 'name': ''} x, 即y\( _1 \)=-x, 当-2\( ≤ \)x<0时, y\( _1 \)随x的增大而______, 且y\( _1 \)>0; 对于函数y\( _2 \)=x\( ^2 \)-x+1, 当-2\( ≤ \)x<0时, y\( _2 \)随x的增大而______, 且y\( _2 \)>0; 结合上述分析, 进一步探究发现, 对于函数y, 当-2\( ≤ \)x\( < \)0时, y随x的增大而 ______ (2)当x\( ≥ \)0时,
对于函数y, 当x\( ≥ \)0时, y与x的几组对应值如下表:
结合上表, 进一步探究发现, 当x\( ≥ \)0时, y随x的增大而增大 在平面直角坐标系xOy中, 画出当x\( ≥ \)0时的函数y的图象
{'width': 213, 'height': 215, 'name': 'image142.png'}
(3)过点(0, m)(m>0)作平行于x轴的直线l, 结合(1)(2)的分析, 解决问题: 若直线l与函数\( y=1/6 |x|(x^2 -x+1)(x≥ -2) \) 的图象有两个交点, 则m的最大值是______
2. (如图,P是{'width': 28, 'height': 31, 'name': 'image143.png'} 与弦AB所围成的图形的外部的一定点,C是{'width': 28, 'height': 31, 'name': 'image144.png'} 上一动点,连接PC交弦AB于点D.
{'width': 285, 'height': 187, 'name': 'image145.png'} 小腾根据学习函数的经验,对线段PC,PD,AD的长度之间的关系进行了探究. 下面是小腾的探究过程,请补充完整:
(1)对于点C在{'width': 28, 'height': 31, 'name': 'image146.png'} 上的不同位置,画图、测量,得到了线段PC,PD,AD的长度 的几组值,如下表:
在PC,PD,AD的长度这三个量中,确定______的长度是自变量,______的长度和_____________的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;
{'width': 226, 'height': 226, 'name': 'image147.png'}
(3)结合函数图象,解决问题:当PC=2PD时,AD的长度约为______cm.
三、练习提升
考点一:寻找变量间的关系,求函数表达式.
1. 随着海拔高度的升高,大气压强下降,空气中的含氧量也随之下降,即含氧量\( y( g/ m^3 ) \)与大气压强\( x( kPa) \)成正比例关系.当\( x=36( kPa) \)时,\( y=108( g/ m^3 ) \),则\( y \)与\( x \)的函数关系式.
2. 港珠澳大桥于2018年10月24日正式通车.大桥在设计理念、建造技术、施工组织、管理模式等方面进行一系列创新,标志着我国岛隧工程设计施工管理水平走在了世界前列.大桥全长近55km.汽车行驶完全程所需的时间t(h)与行驶的平均速度v(km/h)之间的关系式为.
3. 小明用篱笆围出一块周长为12m的矩形空地做生物试验,已知矩形的一边长为(单位:
m),面积为\( y \)(单位:m\( ^2 \)).则\( y \)与\( x \)的函数关系式为_______ ___,自变量\( x \)的取值范围为___________________,当\( x \)=______时,矩形面积最大,且最大面积为 ______________.
考点二:根据函数图象,判断点的运动情况
{'width': 286, 'height': 142, 'name': 'image148.png'} 1.一个寻宝游戏的寻宝通道
如图 1 所示,通道由在同一平面内的\( AB \),\( BC \),
\( CA \),\( OA \),\( OB \),\( OC \)组成.为记录寻宝者的进行
路线,在\( BC \)的中点\( M \)处放置了一台定位仪器,
设寻宝者行进的时间为\( x \),寻宝者与定位仪器之间
的距离为\( y \),若寻宝者匀速行进,且表示\( y \)与\( x \)的函数关系的图象大致如图 2 所示,则寻宝者的行进路线可能为( ). A. \( A→ O→ B \) B. \( B→ A→ C \) C. \( B→ O→ C \) D. \( C→ B→ O \)
2. 有一圆形苗圃如图1所示,中间有两条交叉过道AB,CD,它们为苗圃\( ⊙ \)O的直径,且ABCD. 入口K位于{'width': 27, 'height': 24, 'name': 'image149.png'} 中点,园丁在苗圃圆周或两条交叉过道上匀速行进.设该园丁行进的时间为x,与入口K的距离为y,表示y与x的函数关系的图象大致如图2所示,则该园丁行进的路线可能是( ). {'width': 400, 'height': 116, 'name': 'image150.png'} A. A\( → \)O\( → \)D B. C\( → \)A\( → \)O\( → \) B C. D\( → \)O\( → \)C D. O\( → \)D\( → \)B\( → \)C
考点三:根据函数图像解决实际问题
{'width': 154, 'height': 106, 'name': 'image151.png'} 1.如图1,一辆汽车从点\( M \)处进入路况良好的立交桥,图2反映了它在进入桥区行驶过程中速度(千米/时)与行驶路程(米)之间的关系.根据图2,这辆车的行车路线最有可能是( )
{'width': 141, 'height': 86, 'name': 'image152.png'}
图1 图2
{'width': 146, 'height': 90, 'name': 'image153.png'} {'width': 143, 'height': 87, 'name': 'image154.png'} {'width': 151, 'height': 94, 'name': 'image155.png'} {'width': 149, 'height': 93, 'name': 'image156.png'} A B C D
{'width': 191, 'height': 175, 'name': 'image157.png'} 2. 某通讯公司推出三种上网月收费方式.这三种收费方式每月所收的费用y(元)与上网时间x(小时)的函数关系如图所示,则下列判断错误的是( )
A.每月上网不足25小时,选择A方式最省钱
B.每月上网时间为30小时,选择B方式最省钱
C.每月上网费用为60元,选择B方式比A方式时间长
D.每月上网时间超过70小时,选择C方式最省钱
3.二十四节气是中国古代劳动人民长期经验积累的结晶,它与白昼时长密切相关.当春分、秋分时,昼夜时长大致相等;当夏至时,白昼时长最长.下图是一年中部分节气所对应的白昼时长示意图.在下列选项中白昼时长超过13小时的节气是( )
{'width': 383, 'height': 158, 'name': 'image158.png'}
A.惊蛰 B.小满 C.秋分 D.大寒
四、课堂总结
本节课你有什么收获,在解决问题中需要注意什么?
第3课时 一次函数的图象和性质
【学习目标】
(1)并理解一次函数解析式y=kx+b(k0)中k,b对一次函数图象的位置和变化趋势的影响.
(2)掌握待定系数法求函数解析式的一般步骤.
(3)会把一些实际问题归结为一次函数问题,并会运用一次函数的图象或一次函数的性质加以解决.
【学习过程】
一、考点精讲
特别地,当b=0时,一次函数成为y=kx(k0),这时,y叫做x{'width': 1, 'height': 1, 'name': 'image159.png'} 的正比例函数.
特别地,正比例函数y=kx(k0)的图象是一条过(0,0)的直线.
3.一次函数y=kx+b(k0)中的k值决定了函数的增减性,b值决定图象与y轴的交点. 当k\( > \)0时, y随x的增大而增大; 当k\( < \)0时, y随x的增大而减小. 直线y=kx+b与y轴交点坐标为(0,b), 与x轴交点坐标为(\( -b/k \),0).
4.用待定系数法求一次函数关系式的一般步骤:
(1)设出函数关系式为y=kx+b(k0).
(2)找到两个已知点的坐标(或其它等价的已知条件),并代入所设函数关系式得到关于k、b的方程组.
(3)解方程组求出k、b的值. (4)把得到的k、b的值代入所设关系式.
5.用函数的观点看方程(组)与不等式
(1) 一次函数与一次方程
解关于x的一元一次方程kx+b=0(k、b为常数,k0)相当于在一次函数y=kx+b的函数值y=0时,求自变量x的值,从图象上看,相当于已知直线y=kx+b,确定它与x轴交点的横坐标.
(2) 一次函数与一元一次不等式
解关于x的一元一次不等式kx+b\( > \)0或kx+b\( < \)0(k、b为常数,k0)相当于一次函数
y=kx+b的函数值y \( > \) 0或y \( < \) 0时,求自变量x的取值范围.
每个二元一次方程组都对应两个一次函数,也对应两条直线.从数的角度看,解方程组相当于考虑自变量为何值时两个函数值相等,以及这两个函数值是何值;从形的角度看,解方程组相当于确定两条直线的交点的坐标.
*6.两条直线的位置与系数的关系 \( ô ¿ l_1 :y_1 =k_1 x+b_1 ,ô¿ l_ 2 :y_ 2 =k_ 2 x+b_ 2 (k_ 1 k_ 2 0) \) \( l_1 l_2 ø∘⇔ \) \( k_1 k_2 \) ;
{'width': 79, 'height': 20, 'name': 'image162.png'} \( k_1 =k_2 b_1 b_2 \)
{'width': 79, 'height': 20, 'name': 'image163.png'} \( k_1 =k_2 b_1 =b_2 \);
{'width': 79, 'height': 20, 'name': 'image164.png'} \( k_1 .k_2 = -1 \) .
二、中考真题
1. (2020北京22题5分)在平面直角坐标系xOy中,一次函数y=kx+b(k0)的图象由函数y=x的图象平移得到,且经过点(1,2).
(1)求这个一次函数的解析式;
(2)当x\( > \)1时,对于x的每一个值,函数y=mx(m0)的值大于一次函数y=kx+b的值,直接写出m的取值范围.
拓展:(3)当x<1时,对于x的每一个值,函数y=x+n的值大于一次函数y=\( 1/2 \)kx+b的值,求n的取值范围.
2.(2016北京21题5分)如图,在平面直角坐标系xOy中,过点A(-6,0)的直线l\( _1 \)与直线l\( _2 \):y=2x相交于点B(m,4).
(1)求直线l\( _1 \)的表达式;
(2)过动点P(n,0)且垂直于x轴的直线与l\( _1 \),l\( _2 \)的交点分别为C,D,当点C位于点D上方时,写出n的取值范围
{'width': 168, 'height': 114, 'name': 'image165.png'} {'width': 168, 'height': 114, 'name': 'image166.png'}
三、练习提升
1.如图,在平面直角坐标系xOy中,直线l:y=-x+b的图象经过边长为2的正方形OABC的顶点B,直线l\( _1 \):y=mx+m+1与直线l的图象交于点D(点D在直线BC的上方),与x轴交于点E,与y轴交于点H. (1)求直线l的解析式 (2)求点E、H的坐标(用m表示); (3)直线BC与直线l\( _1 \)交于点F,若\( ∠ \)BDF=90\( ^∘ \),求m的值; (4)若S\( _△ \)\( _HOE \)\( ≤ \)3,求m的取值范围; (5)若HE<2DH,结合函数图象,求m的取值范围.
2.在平面直角坐标系xOy中,直线y=2x+4与x轴,y轴分别交于点A,B,将直线AB向右平移6个单位长度,得到直线CD,点A平移后的对应点为点D,点B平移后的对应点为点C.
(1)求点C的坐标;
(2)求直线CD的表达式;
(3)若点B关于原点的对称点为点E,设过点E的直线为y=kx+b,与四边形ABCD的边有公共点,
结合函数图象,求k的取值范围.
四、课堂总结
本节课你有什么收获,在解决问题中需要注意什么?
第4课时 一次函数的实际应用
【学习目标】
(1)并理解一次函数解析式y=kx+b(k0)中k,b对一次函数图象的位置和变化趋势的影响.
(2)掌握待定系数法求函数解析式的一般步骤.
(3)会把一些实际问题归结为一次函数问题,并会运用一次函数的图象或性质加以解决.
【学习过程】
一、中考真题
{'width': 139, 'height': 121, 'name': 'image167.png'} 1. (2014北京6题4分)园林队在某公园进行绿化,中间休息了一段时间,已知绿化面积S(单位:平方米)与工作时间t(单位:小时)的函数关系的图象如图所示,则休息后园林队每小时绿化面积为( ) A. 40平方米 B. 50平方米 C. 80平方米 D. 100平方米
{'width': 131, 'height': 115, 'name': 'image168.png'} 2. (2020北京8题2分)有一个装有水的容器,如图所示.容器内的水面高度是10 cm,现向容器内注水,并同时开始计时,在注水过程中,水面高度以每秒0.2 cm的速度匀速增加,则容器注满水之前,容器内的水面高度与对应的注水时间满足的函数关系是( ) A. 正比例函数关系 B. 一次函数关系 C. 二次函数关系 D. 反比例函数关系
3. (2015北京9题3分)一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如下优惠:
{'width': 298, 'height': 103, 'name': 'image169.png'}
例如,购买A类会员年卡,一年内游泳20次, 消费50+25\( × \)20=550元.若一年内在该游泳馆游泳的次数介于45~55次之间,则最省钱的方式为( ) A. 购买A类会员年卡 B. 购买B类会员年卡 C. 购买C类会员年卡 D. 不购买会员年卡
二、练习提升
1.直线y=ax+b过点A(0,2)和点B(﹣3,0),则方程ax+b=0的解是( ) A. x=2 B. x=0 C. x=﹣1 D. x=﹣3 {'width': 170, 'height': 104, 'name': 'image170.png'} 2.如图,直线y=x+b与直线y=kx+6交于点P(3,5), 则关于x的不等式x+b>kx+6的解集是 ____________.
3.已知直线\( y=x-3 \)与\( y=2x+2 \)的交点为(-5,-8) 则方程组\( {[ x-y-3=0; 2x-y+2=0 ]. \)的解是__ ______________.
{'width': 186, 'height': 133, 'name': 'image171.png'} 4.如图,直角坐标系xOy中,一次函数\( y=-1/2 x+5 \)的图象l\( _1 \)分别与x,y轴交于A,B两点,正比例函数的图象l\( _2 \)与l\( _1 \)交于点C(m,4).
(1)求m的值及l\( _2 \)的解析式;
(2)求S\( _△ \)\( _AOC \)﹣S\( _△ \)\( _BOC \)的值;
(3)一次函数y=kx+1的图象为l\( _3 \),且l\( _1 \),l\( _2 \),l\( _3 \)不能 围成三角形,直接写出k的值.
5.我国传统的计重工具秤的应用,方便了人们的生活.如图①,可以用秤砣到秤纽的水平距离,来得出秤钩上所挂物体的重量,称重时,若秤杆上秤砣到秤纽的水平距离为x(厘米)时,秤钩所挂物重为y(斤),则y是x的一次函数.下表中为若干次称重时所记录的一些数据.
{'width': 207, 'height': 130, 'name': 'image172.png'} {'width': 181, 'height': 101, 'name': 'image173.png'} {'width': 261, 'height': 64, 'name': 'image174.png'}
(1)在上表x,y的数据中,发现有一对数据记录错误.在图②中,通过描点的方法,观察判断哪一对是错误的?
(2)根据(1)的发现,问秤杆上秤砣到秤纽的水平距离为16厘米时,秤钩所挂物重是多少?
三、课堂总结
本节课你有什么收获,在解决问题中需要注意什么?
第5课时 反比例函数的图象和性质
【学习目标】
(1)巩固反比例函数的概念,会求反比例函数表达式并能画出图象.
(2)巩固反比例函数图象的变化其及性质并能运用解决某些实际问题
(3)逐步提高观察和归纳分析能力,体验数形结合的数学思想方法.
【学习过程】
一、考点精讲
1. 正比例函数与反比例函数图象的交点问题
已知正比例函数\( y=k_1 x(k_1 0) \), 反比例函数\( y=k_2/x (k_2 0) \),当\( k_1 k_2 <0 \)时,两函数图象无交点;当\( k_1 k_2 >0 \)时,两函数图象有两个交点.
2. 一次函数与反比例函数图象的交点问题 如何求一次函数y=ax+b(a0)与反比例函数y=\( k/x \)(k0)图象的交点 令ax+b=\( k/x \), 此式可化为一元二次方程: ax\( ^2 \)+bx-k=0,设其判别式为\( △ \) \( △ \)>0 两函数图象有两个交点 (两个根即为两个交点的横坐标) \( △ \)<0 两函数图象没有交点 \( △ \)= 0 两函数图象有唯一交点
{'width': 101, 'height': 96, 'name': 'image175.png'} {'width': 101, 'height': 96, 'name': 'image176.png'} 二、中考真题
1. 如图, 在平面直角坐标系xOy中, 正方形OABC的边长为2 写出一个函数y=(k0), 使它的图象与正方形OABC有公共点, 这个函数的表达式为______
2.在平面直角坐标系中,点A\( (ab) \)\( (a> 0b> 0) \)在双曲线\( y= k_1/x \)上.点A关于\( x \)轴的对称点B在双曲线\( y=k_2/x \)上,则\( k_1 +k_2 \)的值为______.
三、练习提升
1.正比例函数\( y=k_1 x \)与反比例函数\( y=k_2/x \)的图象交于A、B两点,若点A的坐标 是(1,2),则点B的坐标是 ___________.(用对称性求点B的坐标)
{'width': 227, 'height': 200, 'name': 'image177.png'} 2.如图,在平面直角坐标系\( xOy \)中,一次函数\( y=ax +b__ (a 0) \)与反比例函数\( y=k/x_ k 0 \)的图象交于点A(4,1)和B(\( -1 \),\( n \)).
(1)求n的值和直线\( y=ax +b \)的表达式;
(2)根据这两个函数的图象,直接写出
不等式 \( ax+b-k/x <0 \)的解集.
3.在平面直角坐标系\( xOy \)中,直线l:\( y=ax+b \)与双曲线\( y=k/x \)交于点A(1,m)和B(\( -2 \),\( -1 \)).点A关于x轴的对称点为点C.
(1)①求k的值和点C的坐标; ②求直线l的表达式;
{'width': 159, 'height': 161, 'name': 'image178.png'} (2)过点B作y轴的垂线与直线AC交于点D,经过点C的直线与直线BD交于点E.若 30\( ^∘ \)\( ≤ \)\( ∠ \)CED\( ≤ \)45\( ^ ∘ \),直接写出点E的横坐标t的取值范围.
4.如图,在平面直角坐标系xOy中,函数\( y=k/x(x<0) \)的图象经过点\( A(-1 6) \),直线\( y=mx-2 \)与x轴交于点\( B(-1 0) \).
(1)求k,m的值;
{'width': 199, 'height': 229, 'name': 'image179.png'} (2)过第二象限的点P\( (n-2n ) \)作平行于x轴的直线,交直线\( y=mx-2 \)于点C,交函数\( y=k/x(x<0) \)的图象于点D.
①当\( n=-1 \)时,判断线段PD与PC的数量关系,并说明理由;
②若\( PD ≥ 2PC \),结合函数的图象,直接写出n的取值范围.
四、课堂总结
本节课你有什么收获,在解决问题中需要注意什么?
第6课时 一次函数与反比例函数结合
【学习目标】
(1)综合运用一次函数和反比例函数图象的变化其及性质并能运用解决问题
(2)逐步提高观察和归纳分析能力,体验数形结合的数学思想方法.
【学习过程】
一、中考真题
1. 在平面直角坐标系xOy中, 直线\( y=x \)与双曲线\( y=m/x \)交于A, B两点若点A, B的纵坐标分别为y\( _1 \), y\( _2 \), 则\( y_1 +y_2 \)的值为______
2.在平面直角坐标系xOy中, 直线y=kx+b(k0)与双曲线y=的一个交点为P(2, m), 与x轴、 y轴分别交于点A, B.
(1)求m的值;
(2)若PA=2AB, 求k的值
3. 如图,在平面直角坐标系xOy中,函数y=(x\( > \)0)的图象与直线y=x-2交于点A(3,m).
(1)求k,m的值;
{'width': 178, 'height': 197, 'name': 'image180.png'} {'width': 178, 'height': 197, 'name': 'image181.png'} (2)已知点P(n,n)(n\( > \)0),过点P作平行于x轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数y=(x\( > \)0)的图象于点N.
①当n=1时,判断线段PM与PN的数量关系,并说明理由;
②若PN\( ≥ \)PM,结合函数的图象,直接写出n的取值范围.
二、练习提升
1.在平面直角坐标系xOy中,函数y=\( m/x \) (x>0)的图象过点(1,2)与直线l\( _1 \):y=\( 1/3 \)x+k(k>0)交于点A,与直线l\( _2 \):x=k交于点B,直线l\( _1 \)与l\( _2 \)交于点C. (1)求反比例函数解析式; (2)当点A的横坐标为1时,求此时k的值; (3)连接OB、OC,若S\( _△ \)\( _OBC \)=\( 1/2 \),求点B的坐标; (4)设直线l\( _2 \)与x轴交于点D. \( ① \)当k=\( √(3) \)时,判断线段BC与BD的数量关系,并说明理由; \( ② \)若BC>BD,结合函数图象,求k的取值范围; \( ③ \)若BC\( ≤ \)2BD,结合函数图象,求k的取值范围. 2. 在平面直角坐标系xOy中,已知直线y=\( 1/2 \)x+2与直线y=-x+m交于点A( \( 2/3 \),n), (1)求m,n的值;
(2)若点B是直线y=\( 1/2 \)x+2上一动点,过点B分别作x轴,y轴的垂线,垂足分别为点C和点D,反比例函数y= \( k/x \)的图象经过点 B. \( ① \)当点B与点A重合时,求BC+BD的长; \( ② \)当BC+BD<3时,直接写出k的取值范围.
三、课堂总结
本节课你有什么收获,在解决问题中需要注意什么?
第7课时 二次函数的图象和性质
【学习目标】
(1)理解二次函数的概念、图象、性质及平移规律
(2)理解二次函数的三种形式
(3)会用待定系数法求二次函数的解析式
(4)理解二次函数与一元二次方程之间的关系;
(5)会结合方程根的性质、一元二次方程根的判别式,判定抛物线与 轴的交点情况;
(6)会利用二次函数的图象及性质解决有关问题
【学习过程】
一、考点精讲
(一)二次函数的定义:
形如y= (a0,a,b,c为常数)的函数称为二次函数.其中a为二次项系数,b为 项系数,c为 项.
(二)二次函数的图象及画法
二次函数y=ax\( ^2 \)+bx+c(a0)的图象是对称轴 于y轴(或是y轴本身)的抛物线.几个不同的二次函数.如果二次项系数a相同,那么其图象的开口方向、形状完全 ,只是顶点的 不同. (1)用描点法画图象 首先确定二次函数的开口方向、对称轴、顶点坐标,然后在对称轴两侧,以顶点为中心,左右对称地画图.画结构图时应抓住以下几点:对称轴、顶点、与x轴的交点、与y轴的交点. (2)用平移法画图象 由于a相同的抛物线y=ax\( ^2 \)+bx+c的开口及形状完全相同,故可将抛物线y=ax\( ^2 \)的图象平移得到a值相同的其它形式的二次函数的图象.步骤为:利用配方法或公式法将二次函数化为y=a(x-h)\( ^2 \)+k的形式,确定其顶点(h,k),然后做出二次函数y=ax\( ^2 \)的图象.将抛物线y=ax\( ^2 \)平移,使其顶点平移到(h,k). 平移方法: ________________________________
(三)二次函数
=
+
+
(
0)的图象与性质
二次函数y=ax\( ^2 \)+bx+c(a0)的图象是一条抛物线.它的顶点坐标是 ,对称轴是直线 .
(四)抛物线
=
+
+
中
、
、
的作用
(五)二次函数解析式的确定
一般来说,二次函数的解析式常见有以下几种形式. (1)一般式:y= (a,b,c为常数,a0) (2)顶点式:y= (a,h,k为常数,a0) 要确定二次函数解析式,就是要确定解析式中的待定系数(常数),由于每一种形式中都含有三个待定系数,所以用待定系数法求二次函数的解析式,需要已知三个独立条件. 当已知抛物线上任意三点时,通常设函数解析式为一般式y=ax\( ^2 \)+bx+c,然后列出三元一次方程组求解. 当已知抛物线的顶点坐标和抛物线上另一点时,通常设函数解析式为顶点式y=a(x-h)\( ^2 \)+k求解. (3)交点式:y= (a0),其中x\( _1 \)、x\( _2 \)为抛物线与x轴交点的横坐标.
(六)二次函数与一元二次方程的关系
(1)函数\( y=ax^2 +bx+c(a 0) \),当\( y=0 \)时,得到一元二次方程\( ax^2 +bx+c=0(a 0) \),那么一元二次方程的解就是二次函数的图象与x轴交点的 坐标,因此二次函数图象与x轴的交点情况决定一元二次方程根的情况. ①当二次函数的图象与x轴有 交点,这时\( Δ =b^2 -4ac>0 \),则方程有 实根; ②当二次函数的图象与x轴有 交点,这时\( Δ =b^2 -4ac=0 \),则方程有 实根; ③当二次函数的图象与x轴 交点,这时\( Δ =b^2 -4ac<0 \),则方程 实根. 通过下面表格可以直观地观察到二次函数图象和一元二次方程的关系:
二、中考真题
知识点一:二次函数的图象与性质
1.抛物线y=(x-2)\( ^2 \)+1的顶点坐标是( ) A. (2,1) B. (-2,1) C. (-2,-1) D. (1,2)
{'width': 120, 'height': 140, 'name': 'image182.png'} 2. 下列关于抛物线y=x\( ^2 \)+bx-2的说法正确的是( )
A. 抛物线的开口方向向下
B. 抛物线与y轴交点的坐标为(0,2)
C. 当b>0时,抛物线的对称轴在y轴右侧
D. 对于任意的实数b,抛物线与x轴总有两个公共点
3.函数y=ax\( ^2 \)+bx+c(0\( ≤ \)x\( ≤ \)3)的图象如图所示,则该函数的最小值是________.
4. 已知函数y=kx\( ^2 \)+(2k+1)x+1(k为实数).
(1)对于任意实数k,函数图象一定经过点(-2,-1)和点 ________;
(2)对于任意正实数k,当x>m时,y随着x的增大而增大,写出一个满足题意的m的值为 ____.
知识点二:二次函数解析式的确定
5.请写出一个开口向上,并且与y轴交于点(0,1)的抛物线的解析式___.
6.老师给出一个二次函数,甲、乙、丙、丁四名同学各指出这个函数的一个性质.甲:函数图象不经过第三、四象限;乙:当x<1时,y随x的增大而减小;丙:函数有最小值;丁:当x1时,y>0.已知这四位同学的描述都正确,请你写出满足上述所有性质的一个二次函数表达式________ ___________.
知识点三:二次函数的对称性问题
{'width': 152, 'height': 154, 'name': 'image183.png'} 7. (2018北京7题2分)跳台滑雪是冬季奥运会比赛项目之一,运动员起跳后的飞行路线可以看作是抛物线的一部分,运动员起跳后的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系y=ax\( ^2 \)+bx+c(a0).如图记录了某运动员起跳后的x与y的三组数据,根据上述函数模型和数据,可推断出该运动员起跳后飞行到最高点时,水平距离为( ) A. 10 m B. 15 m C. 20 m D. 22.5 m
三、练习提升
1. 抛物线y=(x-m)\( ^2 \)+m-3(m>0)与x轴交于A(1,0).
(1)求m的值; (2)列表、描点并画出函数图象; (3)求抛物线与y轴的交点; (4)求抛物线的顶点坐标; (5)将抛物线向上平移1个单位,求平移后的抛物线与x轴的交点; (6)当抛物线在x轴下方时,求x轴的取值范围; (7)当函数的值随x的增大而增大时,求x的取值范围; (8)若抛物线上有两点P(x\( _1 \),y\( _1 \)),Q(x\( _2 \),y\( _2 \)),若y\( _1 \)=y\( _2 \),求x\( _1 \)+x\( _2 \)的值.
2. 已知抛物线y=-2x\( ^2 \)+bx-c的顶点坐标为(2,-1),求抛物线的表达式.
3. 已知抛物线y=ax\( ^2 \)+bx-3与x轴的两个交点坐标分别为(-1,0),(3,0),求抛物线的表达式.
4. 已知抛物线y=x\( ^2 \)+bx+c的图象经过(1,6)、(-3,2)两点,请求出该抛物线的表达式,并直接写出它与y轴的交点的坐标.
5. 已知抛物线y=ax\( ^2 \)+bx+c的图象经过(-1、0)、(3、0)、(0、3)三点,求抛物线的表达式.
6. 我们定义一种新函数:形如y={'width': 152, 'height': 154, 'name': ''} ax\( ^2 \)+bx+c{'width': 152, 'height': 154, 'name': ''} (a0,且b\( ^2 \)-4ac>0)的函数叫做鹊桥函数.小丽同学画出了鹊桥函数y={'width': 152, 'height': 154, 'name': '\n'} x\( ^2 \)-2x-3{'width': 152, 'height': 154, 'name': ''} 的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为(-1,0),(3,0)和(0,3);②图象具有对称性,对称轴是直线x=1;③当-1\( ≤ \)x\( ≤ \)1或x\( ≥ \)3时,函数值y随x的增大而增大;④当x=-1或x=3时,函数的最小值是0;⑤当x=1时,函数的最大值是4.其中正确结论的个数是 ____________.
{'width': 143, 'height': 144, 'name': 'image184.png'}
四、课堂总结
本节课你有什么收获,在解决问题中需要注意什么?
第8课时 二次函数的综合应用
【学习目标】
(1)熟练运用函数相关知识分析具体二次函数的图象和性质
(2)通过在复杂情景中抽象出函数模型,并转化成已学知识与方法,体会用数形结合的思想解决函数问题的优越性
(3)透过现象看到二次函数的对称本质,进行有依据的分析,通过数和形两个角度解决问题
【学习过程】
一、函数微技能
练习一 根据二次函数对称性、增减性解答下列问题.
1. 抛物线y=ax\( ^2 \)+bx+c过点A(1,0)、B(3,0),则此抛物线的对称轴是直线 ________.
2. 已知抛物线y=\( 3/4 \)(x-3)\( ^2 \)-3与x轴的一个交点为(1,0),则图象与x轴的另一个交点坐标是 _______
3. 如图,已知抛物线y=ax\( ^2 \)+bx+3(a0)的对称轴为x=2,抛物线与y轴交于A点,过A作x轴的平行线,交抛物线于B点,则B点坐标是 ________.
4. 二次函数y=ax\( ^2 \)+bx+c,当x=m和x=n时(mn),y值相等,则该二次函数的对称轴为__________(用含m,n的式子表示).
5. 已知抛物线y=ax\( ^2 \)+bx+c(a>0)与x轴交于(-1,0),(5,0)两点,当自变量x=1时,函数值为y\( _1 \),当x=3时,函数值为y\( _2 \),则y\( _1 \)_ _______y\( _2 \).(填>,<或=)
6. 已知二次函数y=x\( ^2 \)-4x-1,函数值y的取值范围是 ________,当0\( ≤ \)x\( ≤ \)5时,函数值y的取值范围是_ _________.
7. 二次函数y=(x+1)\( ^2 \)-1,当1<y<2时,x的取值范围是 ___________
8. 已知点P(x\( _0 \),m)和Q(2,n)为抛物线y=x\( ^2 \)-6x+5上两点,若m>n,求x\( _0 \)的取值范围.
9. 当-2\( ≤ \)x\( ≤ \)1时,二次函数y=-(x-m)\( ^2 \)+m\( ^2 \)+1最大值为4,求实数m的值.
练习二 解读下列含参数的二次函数解析式并画出函数草图.
1. 已知抛物线y=x\( ^2 \)-2x+m-3,配方后解析式为_______ ___________,抛物线对称轴为__________,顶点坐标为___________,抛物线顶点在 __________________上运动.分别画出抛物线过点(0,2)和点(0,-1)时的函数图象.
2. 已知抛物线y=x\( ^2 \)-2mx+m\( ^2 \)-2,配方后解析式为 ______________,抛物线对称轴为___________,顶点坐标为________ _,抛物线顶点在____________上运动. 分别画出抛物线过点(0,-1)时,对称轴在y轴左侧和y轴右侧的函数图象.
二、设问突破
1. 在平面直角坐标系中,抛物线y=x\( ^2 \)-2ax+3与y轴交于点C.
(1)若抛物线与x轴正半轴交于点A、B(点A在点B左侧),且OA+OB=4,求a的值;
(2)点P为y轴上一点,P(0,t)(t<3),过点P且垂直于y轴的直线l与抛物线交于Q,R两点,若 PQ+PR=6,求点P的纵坐标t的取值范围.
2. 在平面直角坐标系xOy中,抛物线y=mx\( ^2 \)-2mx-2m+1与x轴交于点A,B(点A、B不重合).
(1)若AB=2,求m的值;
(2)过点P(0,2)作与x轴平行的直线,交抛物线于点M,N.当MN\( ≥ \)2时,求m的取值范围.
三、对接中考
1. (2017北京27题7分)在平面直角坐标系xOy中,抛物线y=x\( ^2 \)-4x+3与x轴交于点A,B(点A在点B的左侧),与y轴交于点C.
(1)求直线BC的表达式;
(2)垂直于y轴的直线l与抛物线交于点P(x\( _1 \),y\( _1 \)),Q(x\( _2 \),y\( _2 \)),与直线BC交于点N(x\( _3 \),y\( _3 \)).若x\( _1 \)<x\( _2 \)<x\( _3 \),结合函数的图象,求x\( _1 \)+x\( _2 \)+x\( _3 \)的取值范围.
2. (2020北京26题6分)在平面直角坐标系xOy中,M(x\( _1 \),y\( _1 \)),N(x\( _2 \),y\( _2 \))为抛物线y=ax\( ^2 \)+bx+c(a\( > \)0)上任意两点,其中x\( _1 \)\( < \)x\( _2 \).
(1)若抛物线的对称轴为x=1,当x\( _1 \),x\( _2 \)为何值时,y\( _1 \)=y\( _2 \)=c;
(2)设抛物线的对称轴为x=t.若对于x\( _1 \)+x\( _2 \)\( > \)3,都有y\( _1 \)<y\( _2 \),求t的取值范围.
四、课堂总结
本节课你有什么收获,在解决问题中需要注意什么?